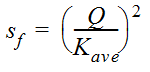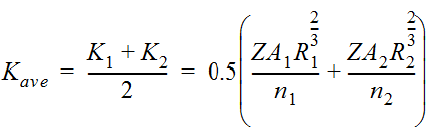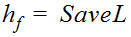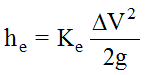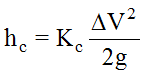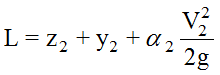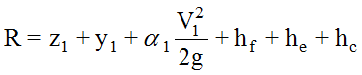Section 6: Channel Analysis Methods
Anchor: #i1018557Introduction
The depth and velocity of flow are necessary for the design and analysis of channel linings and highway drainage structures. The depth and velocity at which a given discharge flows in a channel of known geometry, roughness, and slope can be determined through hydraulic analysis. The following two methods are commonly used in the hydraulic analysis of open channels:
Generally, the Slope Conveyance Method requires more judgment and assumptions than the Standard Step Method. In many situations, however, use of the Slope Conveyance Method is justified, as in the following conditions:
- Anchor: #LGFHNEHH
- standard roadway ditches Anchor: #NJEFMGMI
- culverts Anchor: #IQMGGKKK
- storm drain outfalls.
Slope Conveyance Method
The Slope Conveyance Method, or Slope Area Method, has the advantages of being a relatively simple, usually inexpensive and expedient procedure. However, due to the assumptions necessary for its use, its reliability is often low. The results are highly sensitive to both the longitudinal slope and roughness coefficients that are subjectively assigned. This method is often sufficient for determining tailwater (TW) depth at non-bridge class culvert outlets and storm drain outlets.
The procedure involves an iterative development of calculated discharges associated with assumed water surface elevations in a typical section. The series of assumed water surface elevations and associated discharges comprise the stage-discharge relationship. When stream gauge information exists, a measured relationship (usually termed a “rating curve”) may be available.
You normally apply the Slope Conveyance Method to relatively small stream crossings or those in which no unusual flow characteristics are anticipated. The reliability of the results depends on accuracy of the supporting data, appropriateness of the parameter assignments (n-values and longitudinal slopes), and your selection of the typical cross section.
If the crossing is a more important one, or if there are unusual flow characteristics, use some other procedure such as the Standard Step Backwater Method.
A channel cross section and associated roughness and slope data considered typical of the stream reach are required for this analysis. A typical section is one that represents the average characteristics of the stream near the point of interest. While not absolutely necessary, this cross section should be located downstream from the proposed drainage facility site. The closer to the proposed site a typical cross section is taken, the less error in the final water surface elevation.
You should locate a typical cross section for the analysis. If you cannot find such a cross section, then you should use a “control” cross section (also downstream). (Known hydraulic conditions, such as sluice gates or weirs exist in a control cross section.) The depth of flow in a control cross section is controlled by a constriction of the channel, a damming effect across the channel, or possibly an area with extreme roughness coefficients.
The cross section should be normal to the direction of stream flow under flood conditions.
After identifying the cross section, apply Manning’s roughness coefficients (n-values). (See Equation 6-3 and Chapter 6 for more information.) Divide the cross section with vertical boundaries at significant changes in cross-section shape or at changes in vegetation cover and roughness components. (See Chapter 6 for suggestions on subdividing cross sections.)
Manning’s Equation for Uniform Flow (see Chapter 6 and Equation 6-3) is based on the slope of the energy grade line, which often corresponds to the average slope of the channel bed. However, some reaches of stream may have an energy gradient quite different from the bed slope during flood flow.
Determine the average bed slope near the site. Usually, the least expensive and most expedient method of slope-determination is to survey and analyze the bed profile for some distance in a stream reach. Alternately, you may use topographic maps, although they are usually less accurate.
Anchor: #i1018662Slope Conveyance Procedure
The calculation of the stage-discharge relationship should proceed as described in this section. The Water Surface Elevation tables represent the progression of these calculations based on the cross section shown in Figure 7-14. The result of this procedure is a stage-discharge curve, as shown in Figure 7-15. You can then use the design discharge or any other subject discharge as an argument to estimate (usually done by interpolation) an associated water surface elevation.
- Anchor: #LGNMJLGM
- Select a trial starting depth and apply it to a plot of the cross section. Anchor: #HHNNMEHK
- Compute the area and wetted perimeter weighted n-value (see Chapter 6) for each submerged subsection. Anchor: #OJKINHJK
- Compute the subsection discharges with Manning’s Equation. Use the subsection values for roughness, area, wetted perimeter, and slope. (See Equation 7-1). The sum of all of the incremental discharges represents the total discharge for each assumed water surface elevation. Note. Compute the average velocity for the section by substituting the total section area and total discharge into the continuity equation. Anchor: #KTLFEHJN
-
Equation 7-4.
Anchor: #QIEEEFIE - Tabulate or plot the water surface elevation and resulting discharge (stage versus discharge). Anchor: #KJKHFEGE
- Repeat the above steps with a new channel depth, or add a depth increment to the trial depth. The choice of elevation increment is somewhat subjective. However, if the increments are less than about 0.25 ft. (0.075 m), considerable calculation is required. On the other hand, if the increments are greater than 1.5 ft. (0.5 m), the resulting stage-discharge relationship may not be detailed enough for use in design. Anchor: #RNGNGIKE
- Determine the depth for a given discharge by interpolation of the stage versus discharge table or plot.
The following x and y values apply to Figure 7‑14:
|
X |
Y |
|---|---|
|
0 |
79 |
|
2 |
75 |
|
18 |
72 |
|
20 |
65 |
|
33 |
65 |
|
35 |
70 |
|
58 |
75 |
|
60 |
79 |
Figure 7-14. Slope Conveyance Cross Section
|
|
Subsection L |
Subsection C |
Subsection R |
Full Section |
|---|---|---|---|---|
|
Area (ft2) |
0 |
13.34 |
0 |
13.34 |
|
Wetted Perimeter (ft) |
0 |
15.12 |
0 |
|
|
Hydraulic Radius (ft) |
|
0.88 |
|
|
|
n |
0.060 |
0.035 |
0.060 |
|
|
Q (cfs) |
|
10.43 |
|
10.43 |
|
Velocity (fps) |
|
0.78 |
|
0.78 |
|
|
Subsection L |
Subsection C |
Subsection R |
Full Section |
|---|---|---|---|---|
|
Area (ft2) |
92.00 |
226.00 |
153.50 |
471.5 |
|
Wetted Perimeter (ft) |
20.75 |
25.67 |
28.01 |
|
|
Hydraulic Radius (ft) |
4.43 |
8.81 |
5.48 |
|
|
n |
0.060 |
0.035 |
0.060 |
|
|
Q (cfs) |
122.98 |
818.33 |
236.34 |
1177.66 |
|
Velocity (fps) |
1.34 |
3.62 |
1.54 |
2.50 |
Figure 7-15. Stage Discharge Curve for Slope Conveyance
Anchor: #i1018740Standard Step Backwater Method
The Step Backwater Method, or Standard Step Method, uses the energy equation to “step” the stream water surface along a profile (usually in an upstream direction because most Texas streams exhibit subcritical flow). This method is typically more expensive to complete but more reliable than the Slope-Conveyance Method.
The manual calculation process for the Standard Step Method is cumbersome and tedious. With accessibility to computers and the availability of numerous algorithms, you can accomplish the usual channel analysis by Standard Step using suitable computer programs.
A stage-discharge relationship can be derived from the water surface profiles for each of several discharge rates.
Ensure that the particular application complies with the limitations of the program used.
Use the Standard Step Method for analysis in the following instances:
- Anchor: #HKKFJMNH
- results from the Slope-Conveyance Method may not be accurate enough Anchor: #LMIMMNNN
- the drainage facility’s level of importance deserves a more sophisticated channel analysis Anchor: #SFMLGJNL
- the channel is highly irregular with numerous or significant variations of geometry, roughness characteristics, or stream confluences Anchor: #EFFIIMEF
- a controlling structure affects backwater.
This procedure applies to most open channel flow, including streams having an irregular channel with the cross section consisting of a main channel and separate overbank areas with individual n-values. Use this method either for supercritical flow or for subcritical flow.
Anchor: #i1018812Standard Step Data Requirements
At least four cross sections are required to complete this procedure, but you often need many more than three cross sections. The number and frequency of cross sections required is a direct function of the irregularity of the stream reach. Generally speaking, the more irregular the reach, the more cross sections you may require. The cross sections should represent the reach between them. A system of measurement or stationing between cross sections is also required. Evaluate roughness characteristics (n-values) and associated sub-section boundaries for all of the cross sections. Unfortunately, the primary way to determine if you have sufficient cross sections is to evaluate the results of a first trial.
The selection of cross sections used in this method is critical. As the irregularities of a stream vary along a natural stream reach, accommodate the influence of the varying cross-sectional geometry. Incorporate transitional cross sections into the series of cross sections making up the stream reach. While there is considerable flexibility in the procedure concerning the computed water surface profile, you can use knowledge of any controlling water surface elevations.
Anchor: #i1018827Standard Step Procedure
The Standard Step Method uses the Energy Balance Equation, Equation 6-11, which allows the water surface elevation at the upstream section (2) to be found from a known water surface elevation at the downstream section (1). The following procedure assumes that cross sections, stationing, discharges, and n-values have already been established. Generally, for Texas, the assumption of subcritical flow will be appropriate to start the process. Subsequent calculations will check this assumption.
- Anchor: #LOKGHGKI
- Select the discharge to be used. Determine a starting water surface elevation. For subcritical flow, begin at the most downstream cross section. Use one of the following methods to establish a starting water surface elevation for the selected discharge: a measured elevation, the Slope-Conveyance Method to determine the stage for an appropriate discharge, or an existing (verified) rating curve. Anchor: #HHPMHLKH
- Referring to
Figure
6-1 and
Equation
6-11, consider the downstream water surface to be section
1 and calculate the following variables:
-
Anchor: #GIENJHLL
- z1 = flowline elevation at section 1 Anchor: #LRJIIGFM
- y1 = tailwater minus flowline elevation Anchor: #KJOEJKII
- α = kinetic energy coefficient (For simple cases or where conveyance does not vary significantly, it may be possible to ignore this coefficient.)
Anchor: #JUGGELNL - From cross section 1, calculate the area, A1. Then use Equation 6-1 to calculate the velocity, v1, for the velocity head at A1. The next station upstream is usually section 2. Assume a depth y2 at section 2, and use y2 to calculate z2 and A2. Calculate, also, the velocity head at A2. Anchor: #LPMJIKJJ
- Calculate the friction slope (sf)
between the two sections using Equation 7-5 and Equation 7-6:
Equation 7-5.
where:
Equation 7-6.
Anchor: #NJHKGFKF - Calculate the friction head losses (hf)
between the two sections using
Equation 7-7.
where:
- Anchor: #NLEFLMMI
- L = Distance in ft. (or m) between the two sections
Anchor: #ELTLIEIL - Calculate the kinetic energy correction
coefficients (
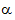 1 and
1 and 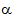 2) using
Equation
6-10.
Anchor: #JGLFIMHK
2) using
Equation
6-10.
Anchor: #JGLFIMHK - Where appropriate, calculate expansion
losses (he) using Equation 7‑8 and contraction
losses (hc) using Equation 7-9 (Other losses,
such as bend losses, are often disregarded as an unnecessary refinement.)
Equation 7-8.
where:
- Anchor: #HRKKEIKF
- Ke = 0.3 for a gentle expansion Anchor: #NHJMKGJI
- Ke = 0.5 for a sudden expansion
Equation 7-9.
where:
- Anchor: #OPLJMIJE
- Kc = 0.1 for a gentle contraction Anchor: #IGPHKEHN
- Kc = 0.3 for a sudden contraction
Anchor: #JFIJIJIE - Check the energy equation for balance
using Equation 7-10 and Equation 7-11.
Equation 7-10.
Equation 7-11.
The following considerations apply:
-
Anchor: #LLKEJJNF
- if L=R within a reasonable tolerance, then the assumed depth at Section 1 is okay. This will be the calculated water surface depth at Section 1; proceed to Step (9) Anchor: #NELKHMKH
- if L≠R, go back to Step (3) using a different assumed depth.
Anchor: #FGIJNENL - Determine the critical depth (dc) at the cross section and find the uniform depth (du) by iteration. If, when running a supercritical profile, the results indicate that critical depth is greater than uniform depth, then it is possible the profile at that cross section is supercritical. For subcritical flow, the process is similar but the calculations must begin at the upstream section and proceed downstream. Anchor: #JMKFINFE
- Assign the calculated depth from Step (8) as the downstream elevation (Section 1) and the next section upstream as Section 2, and repeat Steps (2) through (10). Anchor: #KNKKEHHE
- Repeat these steps until all of the sections along the reach have been addressed.
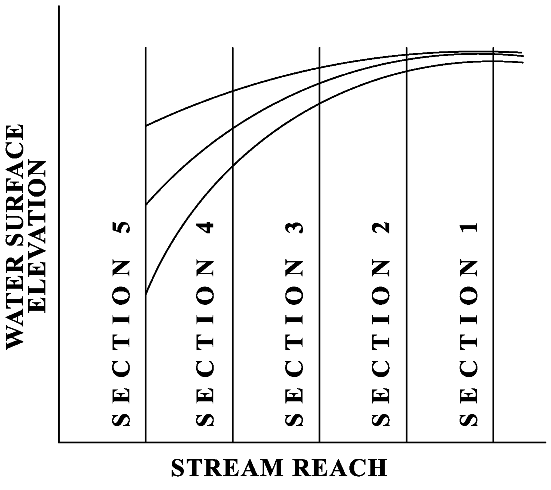
Profile Convergence
When you use the Standard Step Backwater Method and the starting water surface elevation is unknown or indefinite, you can use a computer to calculate several backwater profiles based on several arbitrary starting elevations for the same discharge. If you plot these profiles ,as shown in Figure 7‑16, they will tend to converge to a common curve at some point upstream because each successive calculation brings the water level nearer the uniform depth profile.
Figure 7-16. Water Surface Profile Convergence
The purpose of plotting the curves and finding the convergence point is to determine where the proposed structure site is in reference to the convergence point. If the site is in the vicinity or upstream of the convergence point, you have started the calculations far enough downstream to define a proper tailwater from an unknown starting elevation. Otherwise, you may have to begin the calculations at a point further downstream by using additional cross sections.
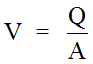
.png)
.png)