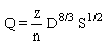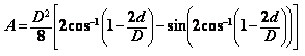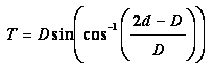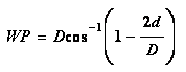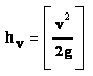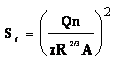Section 2: Flow in Conduits
Anchor: #i1008261Open Channel Flow or Pressure Flow
When a conduit is not submerged, the principles of open channel flow apply. When the conduit is submerged, pressure flow exists because the water surface is not open to the atmosphere, and the principles of conduit flow apply. For circular pipes flowing full, Equation 6‑3 becomes:
Equation 6-16.
where:
- Anchor: #WIVQQPNS
- Q = discharge (cfs or m3/s) Anchor: #QWJTJNIQ
- z = 0.4644 for English measurement or 0.3116 for metric. Anchor: #GIMKQORX
- n = Manning’s roughness coefficient Anchor: #MYQBWFTT
- D = pipe diameter, ft. or m Anchor: #WCEMFCMA
- S = slope of the energy gradeline (ft./ft. or m/m) (For uniform, steady flow, S = channel Anchor: #QRSLIIPW
- slope, ft./ft. or m/m).
Depth in Conduits
The equations for critical depth apply to conduits, too. Determine critical depth for a rectangular conduit using Equation 6-12 and the discharge per barrel. Calculate critical depth for circular and pipe-arch or irregular shapes by trial and error use of Equation 6-13. For a circular conduit, use Equation 6‑17 and Equation 6‑18 to determine the area, A, and top width, T, of flow, respectively. For other shapes, acquire or derive relationships from depth of flow, area, and top width.
Equation 6-17.
Equation 6-18.
where:
- Anchor: #YFYCSHJD
- A = section area of flow, sq. ft. or m2 Anchor: #NLMHIBNI
- T = width of water surface, ft. or m Anchor: #MMIUMPCM
- d = depth of flow, ft. or m Anchor: #MMFLPKRF
- D = pipe diameter, ft. or m Anchor: #WAXIXTJL
- the cos-1 (θ) is the principal value in the range 0 ≤ θ ≤ π.
- Refer to the table below for recommended Manning’s roughness coefficients for conduit. Anchor: #BTNKCMXQ
-
Equation 6-19.
Use Equation 6-3 to determine uniform depth. For most shapes, a direct solution of Equation 6-3 for depth is not possible. The Slope Conveyance Procedure discussed in Chapter 7 is applicable. For rectangular shapes, area, A, and wetted perimeter, WP are simple functions of flow depth. For circular pipe, compute area using Equation 6-17, and compute wetted perimeter using Equation 6-19. For other shapes, acquire or derive the relationship from depth of flow, area, and wetted perimeter.
Anchor: #PRVKSHVNRoughness Coefficients
The following table provides roughness coefficients for conduits.
|
Type of Conduit |
n-Value |
|---|---|
|
Concrete Box |
0.012 |
|
Concrete Pipe |
0.012 |
|
Smooth-lined metal pipe |
0.012 |
|
Smooth lined plastic pipe |
0.012 |
|
Corrugated metal pipe |
0.015-0.027 |
|
Structural plate pipe |
0.027-0.036 |
|
Long span structural plate |
0.031 |
|
Corrugated metal (paved interior) |
0.012 |
|
Plastic |
0.012-0.024 |
Anchor: #i1008037
Energy
The energy equation, Equation 6-6, applies to conduit flow, too. Additionally, the following concepts apply to conduit flow.
- Anchor: #LHNLJICV
- For pressure flow, the depth, d, represents the distance from the flowline to the hydraulic grade line. Anchor: #GJCGWEXF
- For pressure flow, the slope of the energy grade line and hydraulic grade line through the conduit are parallel and are represented by the friction slope. Anchor: #VVIFANJB
- Compute friction losses, hf, as the product of friction slope and length of conduit. Anchor: #LQIVHVJN
- Consider the kinetic energy coefficient (α) equal to unity. Anchor: #PIJFLBOI
- Other losses include entrance losses, exit losses, and junction losses.
Refer to Chapter 8 for directions to accommodate such losses for culvert design and Chapter 10 for storm drain design.
Compute the velocity head at any location in a conduit using Equation 6-20.
where:
Equation 6-20.
where:
- Anchor: #FWEYRMNQ
- v = flow velocity in culvert (ft./s or m/s). Anchor: #SGLIFIKB
- g = the gravitational acceleration = 32.2 ft/ s2 or 9.81 m/s2.
The friction slope represents the slope of the energy grade line and is based upon Manning's Equation, rearranged as follows:
Equation 6-21.
where:
- Anchor: #YFCMIAOB
- Sf = friction slope (ft./ft. or m/m) Anchor: #EXWXJXRQ
- z = 1.486 for English measurements and 1.0 for metric.
Steep Slope versus Mild Slope
When critical depth (dc) is higher than uniform depth (du), the slope is steep. The conduit may flow completely full (pressure flow) or partly full (free surface flow). The free surface flow may be supercritical or subcritical depending on tailwater conditions.
When critical depth is lower than uniform depth, the slope is termed mild. Pressure flow or free surface flow may occur. Free surface flow is most likely to be subcritical within the conduit.
The shape of the free water surface is dependent on whether the conduit slope is steep or mild and on the tailwater conditions. The Standard Step Procedure described in Chapter 7 accommodates the differences in water surface shape.